こんにちは.今回は運動方程式のお話.
運動方程式

って人は教科書呼べば書いてありますので教科書優先で.※全国の井上君名前借りてごめんねっ!

って人は次の「運動方程式を使うコツ」まで飛んでください.
以下私の解釈↓
運動の3法則のうち,第二法則「運動の法則」を使います.運動の3法則はコチラ↓
まず,運動の第二法則「物体の加速度は加えられた力に比例し,物体の質量に反比例する」というのを式にします.
$$a=k \cdot \frac{F}{m}$$
\(a\):加速度
\(k\):比例定数
\(F\):力
\(m\):質量
これを変形して,
$$ma=kF$$
\(m\)=1[kg], \(a\)=1[m/s2]の時,\(F\)=1[N]になるように定義(定数\(k\)=1と定義)したのがお馴染みの運動方程式
$$F=ma$$
です.
加速度をベクトル(符号ありの加速度)と考えた時は,力\(F\)もベクトルになります.
加速度や速度を「こっちが正!」って決めた限りは,力もそれに従うようにします.
運動方程式を使うコツ
コツその1
$$F=ma$$
と,
$$ma=Fの和$$
という二つの式を使い分けます.
\(F=ma\)は,単純に加速度のわかっている物体にかかる力を求めるとき.
\(ma=Fの和\)は,物体の加速度を求めたいときに使います.「物体の質量×加速度」=「物体にはたらく力の和」という式になります.
コツその2
運動方程式は,必ず1つの物体について方程式を立てます.

こっちの物体から作用する力はこれだけどもう一つの物体からも影響受けてるし,そしたらこっちの物体にも力がかかるし…..あれぇぇ?????
っていうの状態になっていたのが私.
他の物体からの力はもちろん考慮します.しかし,自分から他の物体にはたらく力とかは考えちゃだめです!
$$ma=F_1+F_2+\cdots +F_n$$
$$ma=\displaystyle \sum_{i=1}^n F_n$$
コツその3(?)
わかってる人はわかっていると思いますが,運動方程式で使うのは物体の加速度方向の「力」の成分だけです.
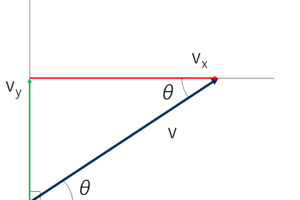
例えば物体が水平方向の加速度を持っていて,斜めに力がかかっている場合なんかは,力を分解して水平方向の成分だけ見てあげましょう.
力の分解がまだあやふやな人はコチラ↓
関連~重力~
地球上の物体には,重力加速度\(g\)[m/s2]が掛かっています.
運動方程式に従えば,物体にかかる重力は
$$F=mg$$になります.
演習を重ねていたら,重力\(=mg\)と言えるくらいになりますので心配しなくてもいいですが,
という本質は頭の片隅に置いておくと困った時の助けになります.






運動方程式ってそもそもなに??