こんにちは！今回は，鉛直投げ上げと鉛直投げ下ろしです．
鉛直投射とは？？
まず鉛直とは？ってところから．
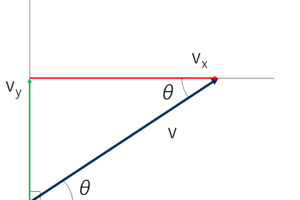
「水平」に対して垂直な向きのことを「鉛直」と呼びます．要するに縦方向のことです．
物理をやるうえでは頻繁に登場するので水平と鉛直は覚えましょう．
鉛直投射は鉛直方向に運動する等加速度直線運動ととらえれば問題ありません．加速度は常に一定(\(g\)[m/s2])です．
与えられる初速度が鉛直上向きの場合は鉛直投げ上げ，鉛直下向きの場合は鉛直投げ下ろしになります．
鉛直投げ上げ
物体を鉛直上向きに投げることです．まっすぐ上向きに物を投げるのが鉛直投げ上げ．
物体は重力加速度がかかるので次第に減速し，そのうち最高点に達して一瞬静止します（一瞬\(v=0\)になる）．
静止した後は自由落下し始めます．
鉛直投げ下ろし
物体を鉛直下向きに投げること．まっすぐ下向きに物を投げるのが鉛直投げ下ろし．
物体は重力加速度がかかるので加速していきます．
空気抵抗を無視しているので，物体は永遠に加速し続けます．
等加速度直線運動の応用で解く
鉛直投げ下ろしも投げ上げも加速度はずっと\(g\)（9.8）m/s2です．
初速度の方向が上か下かの違いだけ．ってことは，単純に初速度のある等加速度運動の式で解けばいいんじゃない？というのが今回のポイント．
等加速度直線運動がまだあやふやな人は復習に読んでおくのがおススメ↓
等加速度直線運動で初速度ありの場合，下の式になりました．
$$x=\displaystyle \frac {1}{2} at^2 + v_0 t$$
\(x\)：距離[m] \(a\)：加速度[m/s2] \(t\)：経過時間[s] \(v_0\)：初速度[m/s]
鉛直投射は，これの加速度\(a\)[m/s2]を\(g\)に代えるだけ．
問題は，正負の設定と距離\(x\)がどうなるかです．
正負の設定
速度も加速度も距離も，本来はベクトルなので符号を考える必要があります．※ベクトルまだ習っていない人すいません…
問題に正負が与えられていない場合は，自分で勝手に正負を決めてしまいます．例えば，今回は直感的にわかりやすいように上向きを正にします．
正負をこの向きで設定すると，重力加速度は下向きなので\(-g\)[m/s2]になります．
\(v_0\)を代入するときも符号付きにするのを忘れずに．
そうすると，正負を考慮した式が出来上がります．
$$x=\displaystyle \frac {1}{2} \cdot (-g)t^2 + v_0 t$$
変位\(x\)←重要！
距離を\(x\)と置いていますが，これはあくまで原点からの距離で，往復した距離や移動した総距離は含めないので要注意．
一言でいえば\(x\)は変位（原点からどれだけ離れているか）を表しているので，移動距離はこの計算方法では出てきません．
鉛直投げ下ろしの時には物体が往復したりしないので変位の大きさと移動距離が等しくなります．が，投げ上げの時は物体が同じ区間を行き来するので変位の大きさと移動距離は一致しません．
実はちょー簡単で，投げ上げの運動を
- 投げ上げてから静止するまで
- 静止した後（落ち始めた後）
に分解して考えます．
静止するまでの運動
まずは静止するまでの時間\(t_1\)を求めます．
初速度\(v_0\)[m/s]と減速した速度\(-gt_1\)[m/s]が等しくなればいいので，
$$v_0+(-gt_1)=0$$
または，
$$v_0=gt_1$$
という等式が成り立ちます．速度は符号ありです．
静止するまでの運動（頂点に達するまでの運動）は，ふつうに初速度のある等加速度運動の式に当てはめればいいだけです．
静止するまでに移動した距離を\(x_1\)，鉛直上向きを正とすると，
$$x_1=\displaystyle \frac {1}{2} \cdot (-g){t_1}^2 + v_0 t$$
になります．
静止後の運動
静止したあと（頂点に達したあと）の運動を考えます．スタートが頂点なので初速度は0の状態．
頂点を距離0として考えていきます．
頂点に達した時から時間\(t\)までかかる時間を\(t_2\)とします．
そうすると，移動した距離\(x_2\)は，
$$x_2=\displaystyle \frac {1}{2} \cdot (-g){t_2}^2$$
という等式になります．
物体は頂点より下に移動するので，距離はマイナスで出てきます．
距離の大きさを求めたいので，絶対値をつけてプラスにしちゃいます．
\(|x_1|\)と\(|x_2|\)を足すと，総距離が計算できます！
文字にすると結構複雑に見えますが，やることは頂点に達する前と後に区間分けして考えるだけ．
