みなさんこんにちは！今回は，力や速度の分解と合成のお話．
力・速度の分解
速度の分解も力の分解もやり方は同じなのでまとめちゃいます．
よく使うのは分解のほう．分解のやり方はしっかり覚えておきましょう．
まずはざっくり手順をまとめてみました．
- 分解する方向を決める
- 元の力（速度）が平行四辺形の対角線になるように，2方向に分解する．
- （分解する2方向が直角なら）θの場所を決める
1.はそのまんまの意味なので軽く解説する程度で．
分解する方向の決定
力や速度を分解する2方向を決めます．
分解する方向は，たいてい力学の場合だと
- 水平方向と鉛直方向
- 斜面方向と斜面垂直方向
の2通りです．分解する2方向が直角なので，最後に「θを決める」作業を行います．
分解（平行四辺形をつくる）
元の速度や力が平行四辺形の対角線になるように分解します．言葉だとわかりづらいと思うのでアニメーションにしました．
こんな感じで，2方向への力・速度の分解が完了します．
が，意外と「どこにどう平行四辺形ができるんだ？？？」って混乱することもあります．
特にテストのときになってテンパるとこういう基本的なところで「？？？？？？」な状態に陥ってしまいます．
ここで超テンパりやすい＆パニクりやすい私の秘儀を紹介していきます．それは….
平行四辺形じゃなくて三角形を作る！！！！
いや，やっていることとしては全くおんなじなんです．平行四辺形だと分解に関係ない余計な2本分まで考えなくてはなりません．頭の弱かった私はこれのせいでパニックに…
とりあえずやり方を紹介します．
- まずは先ほどのとおり，分解する2方向を決めます．
- 片方の辺を平行移動させて矢印の先端まで持ってきます．どっちの辺を持ってきても大丈夫．
- 出来上がった三角形の辺が分解して求めたかった速度や力になります．
- 1点の速度や力を分解しているので，分解した矢印の始点は元の矢印の始点と重ねなければならないので，元の基準線の場所に移動させて完成．
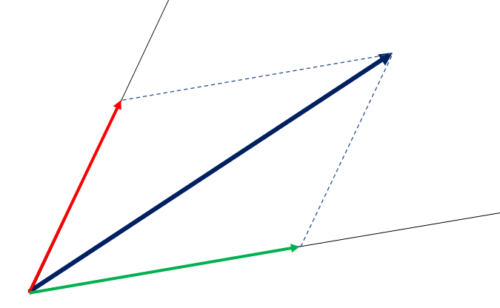
そうすると，2方向に分解できるんです！ちょっと言葉と画像だとわかりにくかったのでアニメーションにしてみました．
やってることは実質平行四辺形を作っているようなもんですが，実際やっていることはベクトルの足し算です．
紙の上でやるときはこんなデジタルにはできないので，鉛筆などで片方の辺を「すーっ」と平行移動させましょう．
あとは元の基準線に戻してあげるだけ．
角θの場所を決める
力や速度の分解でわからないという声の多いのが「どこをθにしていいかわかんない」「どっちがsinでどっちがsinかわかんない」という声です．
もちろんθ以外の角度表記でも当てはまります（\(α，β\)とか).
斜めの力や速度を「水平方向と鉛直方向」に分解したり，鉛直（水平）方向の力や速度を「斜面方向と斜面垂直方向」に分解したりするときは，どこがθなのかを考える必要があります．
地道に三角形の相似を調べるのはバカ臭いので，今回はそれ以外の2通りの方法を教えます．
- さっきの三角形の方法で考える
- 角度を極端に小さく（大きく）した場合を考える
とりあえず文字だけだとわかりにくいので例題を作りましょう！
例題)
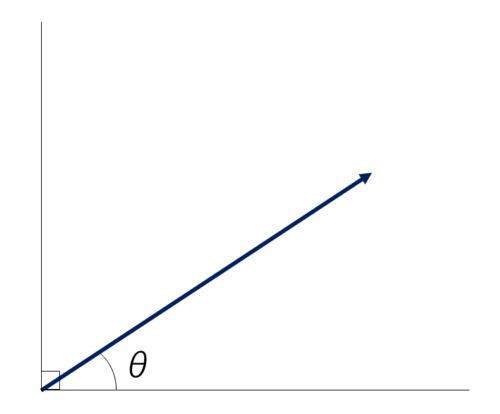
物体が速度\(v\)，水平面から角度\(θ\)の方向に運動している．
水平方向の速度成分\(v_x\)と鉛直方向の速度成分\(v_y\)を求めよ．
三角形の方法でθを決める
まずは分解していきます．
- 分解する方向を決めて
- 片っぽの辺を平行移動させて分解したい矢印に合わせ
- 分解された速度を作る
の手順です．そこまではざっくりアニメーションにしました．
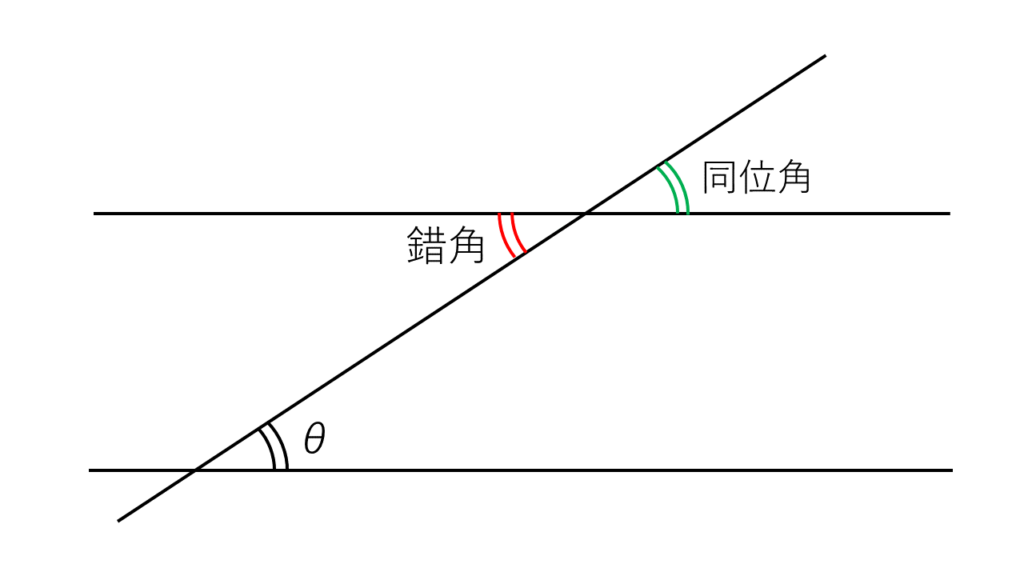
こうやってやると，\(θ\)がどこになるかって，簡単に見えてきませんか？
そう，錯覚の関係にあるので\(θ\)は下の画像の位置になります．
平行な2辺に1つの直線が交わるとき，錯覚・同位角の関係にある角はすべて等しくなります．
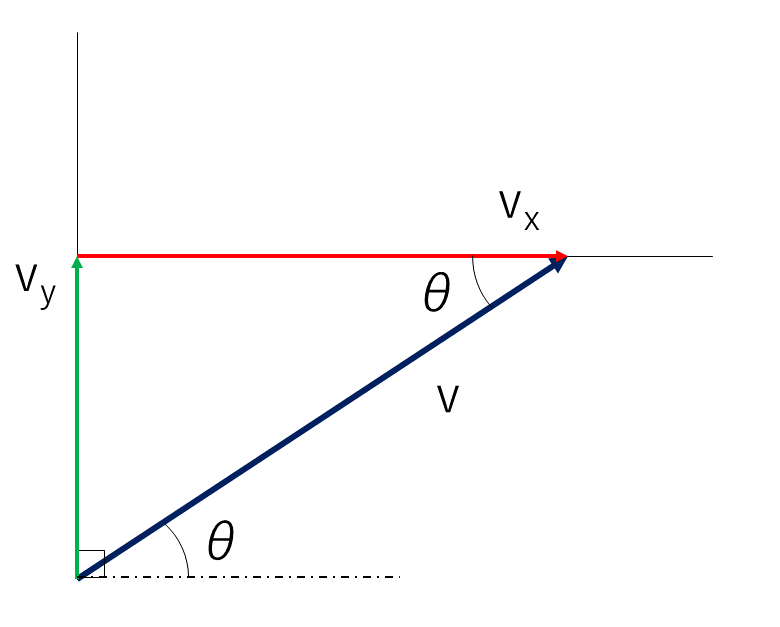
あとは\(v_x\)と\(v_y\)を\(\sinθ\)と\(cosθ\)を使って表すだけ．この場合はsinとcosで迷うことはないと思います．迷ったら次の「角度を小さくする方法」にgo．
ここからは高校1年でやった三角関数レベルで解けますね．（もしかしたら三角関数は2年か？？）
$$v_x=v \cosθ$$
$$v_y=v \sinθ$$
$$終$$
角度を極端に小さく（大きく）する方法
コチラはsinとcosが分かんなくなったときに使います．
まずはふつうに三角形を使っても平行四辺形を使ってもいいので速度を分解します．
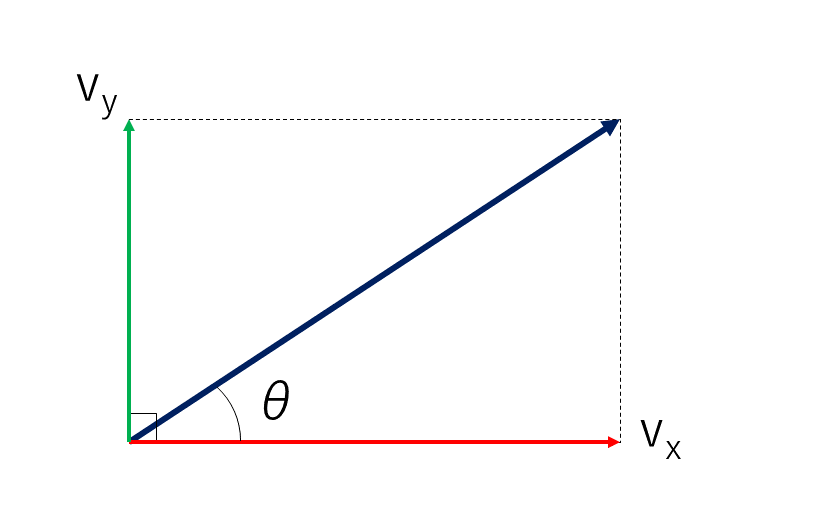
そんで，角度を極端に小さくします．
角度を小さくしたとき，成分も小さくなるほうがsin，逆に成分が大きくなるほうがcosです．
今回の場合は\(v_y\)が極端に小さくなり，\(v_x\)が元の\(v\)に近づき大きくなりますので，
\(v_y\)がsin，\(v_x\)がcosになります．
まとめ
今回の例題は水平方向と鉛直方向だったのでわかりやすかったと思います．
三角形を作る方法は，特に力の分野で分解したい方向が「斜面方向と斜面に垂直な方向」のようなちょっとややこしい問題に使うと説きやすくなるのでお試しあれ！
それでは～👋
お前なにバカな事言ってんだよww