相対速度とは？！これを押さえないと死ぬぞ！

速度についてはもう大丈夫だと思います．

まだ速度すらあやふやだよぉ～～

という人はコチラの記事を先に読んでおいてください↓

力・速度の分解と合成

2020年5月9日

※全国の井上君，名前借りてごめんなさい

相対速度とは？？

相対速度は，ある物体から他の物体を観察したときの速度のこと．

右向きを正として，青い車が+30km/h，黒い車が+45km/hだったら，

• 青い車から見た黒い車の相対速度
  ：+15km/h
• 黒い車から見た青い車の相対速度
  ：-15km/h

これくらいなら何となくわかると思うんですが，これをどう求めたのかを知っておかないと死にます（特にドップラー効果とか）．

相対速度の求め方

まずは一番簡単な例として，2物体が同じ直線上を運動している場合を考えます．

求める手順をまとめてみました．

1. 観測者側（基準）の物体を決める
2. 「相対速度を求めたい物体の速度」から「基準の物体の速度」を引く

簡単な例題を作ったのでやってみましょう．

例題1

赤い物体は15m/s，青い物体は10m/sで，どちらも右向きに運動している．

(1)赤い物体から見た青い物体の相対速度を求めよ．

(2)青い物体から見た赤い物体の相対速度を求めよ．

(3)↓のように速度を文字で置いて，それぞれ文字式で求めよ．

• 赤い物体の速度：\(v_R\)
• 青い物体の速度：\(v_B\)

平面上での相対速度（本題）

平面上でもやることは一緒なんですが，一気に頭が混乱します．

今回は三角形を使った方法とベクトルを使った方法を紹介します．

三角形を使う方法

ざっくり手順だけまとめました

1. 2つの速度を矢印にする
2. 矢印の始点を合わせる
3. 基準になる速度の矢印をひっくり返す
4. 2つの速度を合成する

これだけだとわかりにくいので，例題を使って説明していきます．

例題2

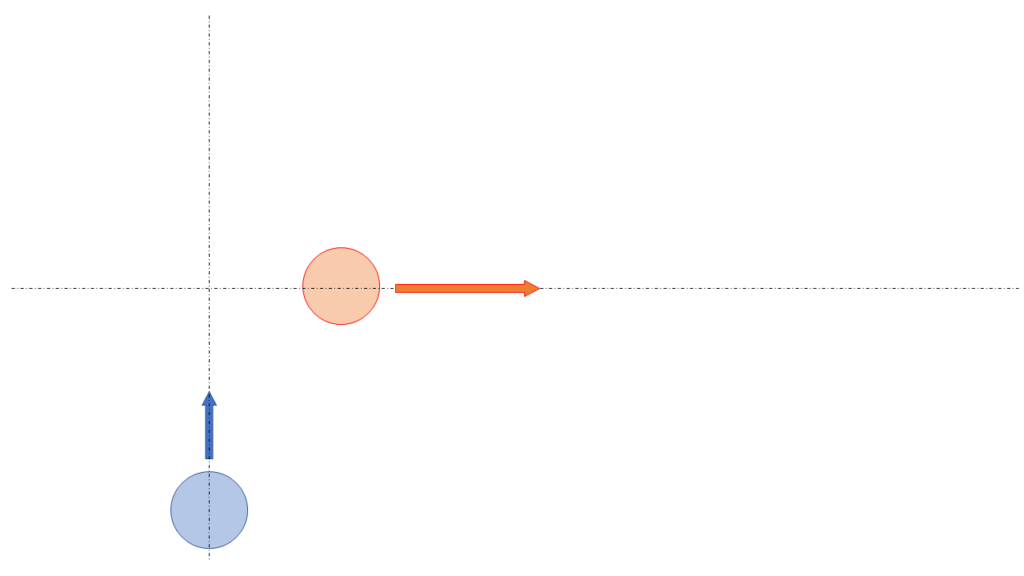
画面上向きに2.0m/sで進む物体A，画面右向きに\(2 \sqrt 3\)m/sで進む物体Bがある．

物体Bから見た物体Aの相対速度を有効数字2桁で求めよ．

また，相対速度の方向を，左向きから何度上向きになっているという形で答えよ．

答え

さっきの手順通りに進めていきます．再生ボタンをタップするとアニメーションが始まります．

相対速度の大きさを求めるときだけ三平方の定理を使います．

$$相対速度^2=Aの速度^2+Bの速度^2$$

代入してあげると，相対速度は

$$v_{A/B}=4.0[ｍ/ｓ]$$

になります．

Aの速度，相対速度，Bの速度は\(1:2:\sqrt3\)の関係になっているので，相対速度の方向は，左向きから30°上向きの方向になります．

どんな作業をしているかは何となくわかってもらえたでしょうか？それでは，次はベクトルを使った計算方法です．

ベクトルを使った方法

同じ直線上を運動する物体の場合は，単純に「相対速度を求めたい物体の速度」から「基準の物体の速度」を引いたものでした．

実は，速度をベクトルとしてとらえると，平面の場合も立体空間の場合も，相対速度は「相対速度を求めたい物体の速度」から「基準の物体の速度」を引く「引き算」で計算できます．

先ほどと同じ例題を，ベクトルを使って解いてみたいと思います．

※ベクトルまだ習っていない人ごめんね

ベクトルの計算についてはコチラにわかりやすい解説が乗っていますので参考までに．

例題3

画面上向きに2.0m/sで進む物体A，画面右向きに\(2 \sqrt 3\)m/sで進む物体Bがある．

物体Bから見た物体Aの相対速度を有効数字2桁で求めよ．

また，相対速度の方向を，左向きから何度上向きになっているという形で答えよ．

答え

さっきと問題は全く一緒です．

まず，速度をベクトルで表さなければなりません．

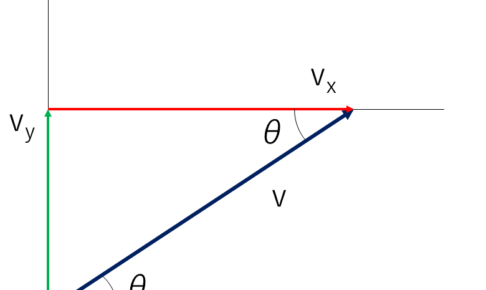
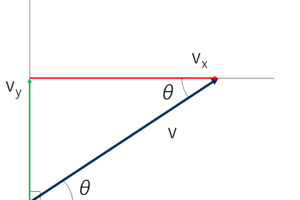
それぞれの物体の速度成分を「垂直方向」と「鉛直方向」に分けて表記します．
上の欄が水平成分，下の欄が鉛直成分とします．

$$\left(
\begin{array}{c}
v_x \\
v_y \\
\end{array}
\right)$$

物体A，Bの速度をベクトルを使って表すと，

$$\vec {v_A}=
\left(\begin{array}{c}
0 \\
2 \\
\end{array}
\right)$$

$$\vec {v_B}=
\left(\begin{array}{c}
0 \\
2 \sqrt{3} \\
\end{array}
\right)$$

となります．

次に「求めたい物体の速度ー基準の物体の速度」をやっていきます．

ベクトルの引き算は，成分(各段)ごとに計算すればいいので，

$$\vec {v_A}- \vec {v_B}$$

$$=\left(\begin{array}{c}
0 \\
2 \\
\end{array}
\right)
–
\left(\begin{array}{c}
2 \sqrt{3}  \\
0 \\
\end{array}
\right)$$

$$=\left(\begin{array}{c}
-2 \sqrt{3} \\
2 \\
\end{array}
\right)$$

このベクトルをグラフにプロットするとこんな感じになります．

先ほどの三角形を使ったやり方と同じ図形になりました．

あとは相対速度のベクトルの大きさを求めてあげればいいだけです．

求め方は三角形の時と一緒で，三平方の定理を使いましょう．

今回はここまで．ベクトル習っていない人は2つ目の解法が分かりにくかったと思います．

こりゃベクトルの解説ページも作らなきゃですね…

それでは．