こんにちは.今回は圧力のお話.
圧力と力の差
先に圧力とはなにか?を知っておく必要があります.
単位面積当たりにかかる力のこと.
$$P= \displaystyle \frac{F}{S}$$
\(P\):圧力[N/m2]
\(F\):力[N]
\(S\):面積[m2]
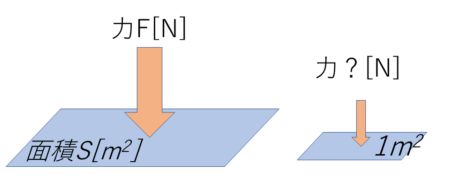
注意:圧力=力ではない!!
圧力と力は,似ているようで違うもの.
「単位面積当たりにかかる『力』って言ったじゃないか!」と思う人もいるかもしれないんですが,圧力は「面積」とセットじゃないと力にはなれないんです.
面積を考慮したのが圧力.面積がどれだけ大きかろうが小さかろうが関係ないのが力.

っていう人向けに解説を.
圧力っていうのは,超簡単に言うとどれくらい物体を押しつぶせるかってことです.わかりやすいようにスポンジの上に物体を乗せる実験をしてみます.

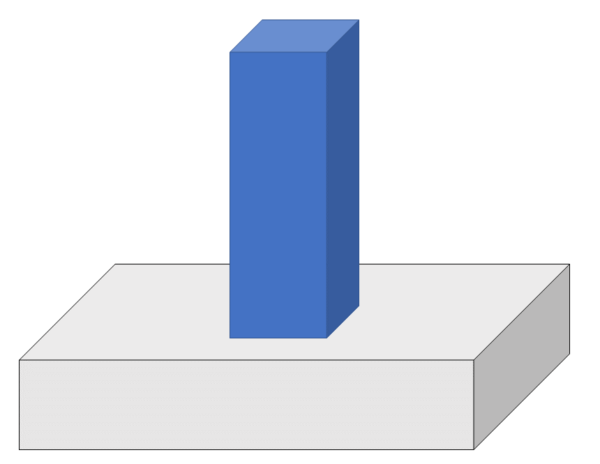
おんなじサイズの物体をスポンジの上に乗っけます.
そうすると…

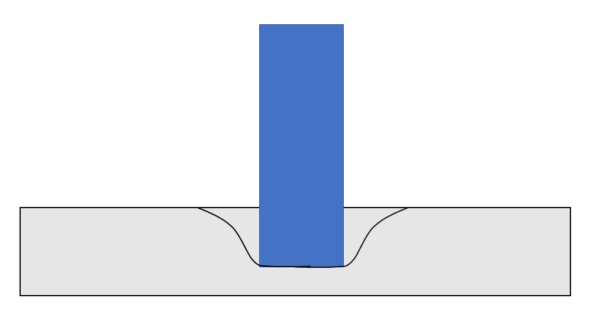
こんな感じに,スポンジのへこむ量が違うのは想像できると思います.
このスポンジをどれくらい凹ませられるかを圧力と呼びます.
※どっちの場合もスポンジにかかる力は同じです.なぜなら同じ重力\(F=mg\)がかかっているから.
スポンジを押す面積が小さければ小さいほどスポンジはへこみ,スポンジを押す力が多きければ大きいほどスポンジはへこみます.
つまり,スポンジのへこむ量は面積に反比例し,力に比例します.←重要
Fが分母?面積が分母?
よく式を丸ごと暗記する人にありがちなんですが,

\(力F\)と\(面積S\),どっちが分子でどっちが分母かわかんなくなっちゃうぅぅぅ!
って人,多いんじゃないでしょうか?

式を丸暗記するのはやめて,圧力って何だったか,そして圧力の定義・単位を思い出しましょう.
スポンジを押す面積が小さいと,小さな力でもスポンジは大きくへこみます.小さくなればなるほどへこます能力(=圧力)は大きくなります.つまり面積と圧力は反比例の関係.
一方,スポンジを押す力が大きくなればなるほど,スポンジをへこませる能力(=圧力)も大きくなります.つまり力と圧力は比例の関係.
ってことで,面積\(S\)が分母,力\(F\)が分子っていうので迷うことはなくなります.
- 圧力:単位面積(大概1m2)あたりに働く力
- 分母と分子こんがらがったらスポンジを思い出して考えてみる
- 力と圧力は別物




何言ってんの???