力学の基本！速度と移動距離

速度とは？

日本語で言えば，決まった時間でどれくらい進めるかってこと．この時「方向も考える」のが速度．方向の概念なしに数字の大きさだけでいいのは「速さ」．

同じ時間で進める距離が大きいほど，同じ時間で長い距離進めるのはわかると思います．二つの物で比較したらどっちが速いっていうのはわかりますが，単体だと明確な基準がないので判断できません．

そこで，基準になる時間を決めて「1時間でどれくらい進める？」「1秒だったらどれだけ進める？」という統一化された数字にしてわかりやすくしたのが速度．

単位時間は1秒だったり1時間だったり1日だったり，とりあえず頭が「1」であればいいんです．高校物理ではよく基準が1秒の「秒速[m/s]」を使います．

速さを\(v\)[m/s]，進んだ距離を\(x\)[m]，かかった時間を\(t\)[s]とすれば，進んだ距離から1秒当たりならどんくらい進む？っていうのを求めることなので，お馴染みの式

$$v= \displaystyle \frac{x}{t}$$

が出来上がります．

ちなみに，何を何で割ればいいかわからなくなったときは，「速度は1秒で進める距離のことだったなぁ」ということだけ覚えておけば，

$$x=vt$$

という式はすぐに思いつくと思います．これを\(v\)について解けば上の式と同じものが得られます．

座標系の導入

定規などで決められた時間にどれくらい進めたかを測ると速さを求めることができました．

ここに座標系を導入してみます．これで物体の進む方向を右向きに動くと+，左向きに動くとマイナスとしてあらわすことができるようになります．

まず，物体が最初にいる場所を原点にします．

続いて，\(t\)秒後に物体が到達した地点の座標を\(x_t\)とします．

そうすると，速度\(v\)は，

$$v[m/s]=\displaystyle \frac{x_t}{t}$$

このとき，\(x\)には符号を含めて代入します．そうしないと，速度ではなく「速さ」が求まってしまいます．

こっちにも先ほどの「速さ」で紹介した，「正しい等式であればどれでも答えがでる」というのは通用します．だから1発でわからなければ\(x=\)の形で等式を作ってもOK．もちろん\(t=\)で式を作ってもOKですが，いきなりこの形にする人はあまりいないでしょう．

加速度とは？

速度の次は加速度です．速度に対してちょっとイメージしづらいのですが，速度が決まった時間でどれだけ変化するかというもの．

一般的に加速度のアルファベットは\(a\)が良く用いられます．

例えば2秒間で速度が4[m/s]速くなったなら，その時の加速度は

$$a=2[m/s^2]$$

になります．1秒間で2[m/s]速くなるよっていうこと．減速していく場合はマイナスがつきます．

「決まった時間当たりのってことは，変化量を時間で割ったんだろ？なんで単位に2乗出てきてんだよ」（s²のこと）と思う人もいるでしょう．

決まった時間当たりの変化量という考え方だと\(v\)/sという表記になりますが，速度ですでに[m/s]という単位になっていますので，そこに[\(\displaystyle \frac{1}{s}\)]が合わさった結果，[m/s²]という形が出来上がります．

等速直線運動と等加速度直線運動

等速直線運動は中学校でもやりましたよね？

物体が同じ速度でまっすぐ運動することです．速度の大きさと時間の関係をグラフにすると↓のような感じになります．

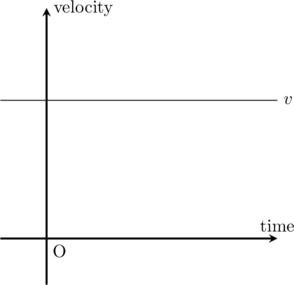
物体が等速直線運動をするとき，物体にはたらく力はすべての方向で釣り合っています．つまり，合力ゼロの状態です．

詳しくは力学・力とモーメントの章に書きます．

等加速度直線運動は，ずっと同じ加速度で直線運動をする状態のこと．

ちょっとわかりづらいかもしれませんが，物体がずーっと加速（減速）し続けながら運動する状態．1秒で速度が変化する割合は常に一定です．

速度の大きさと時間のグラフはこんな感じになります↓

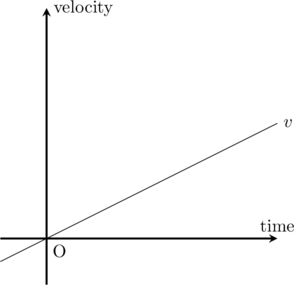
物体が落下するときも等加速度運動をします．1秒間で増加する速度は（空気抵抗を無視すると）常に一定なので，1秒後に9.8[m/s]，2秒後に19.6[m/s]，3秒後に29.4[m/s]と変化していきます．

一秒あたり9.8[m/s]速くなっていくので，物体が落下するときの加速度は9.8[m/s²]になります．詳しくは自由落下のページを見てください．

自由落下

2020年5月6日

時間 t で進める距離

等速直線運動

等速直線運動の場合は，進んだ距離は簡単に

$$x[m]=v[m/s] \times t[s]$$

と式を立てられると思います．

これは，先ほどの\(v-t\)グラフでいう所の\(v\)と\(t\)で囲まれた長方形の面積になります．

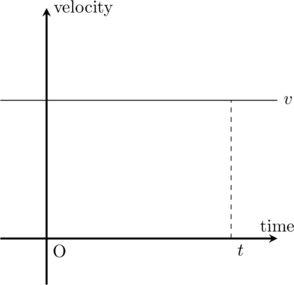
※厳密には\(x,y\)軸にも囲まれていなければなりません．簡単のために省略．

等加速度直線運動

一方等加速度運動の距離を求める式は，直感では導出できないと思います．

初速度が0のときの等加速度直線運動

観測を始めた時の速度（初速度）が0の場合，等速直線運動の場合と同様に，進んだ距離は\(v-t\)グラフ（速度と時間の関係を表すグラフ）の\(v\)と\(t\)で囲まれた図形（三角形）の面積を求めることになります．

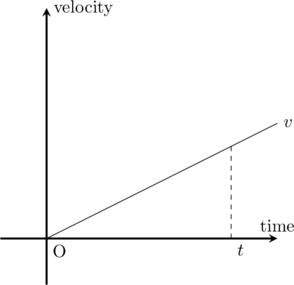
三角形の面積の公式に当てはめると，進んだ距離\(x\)は，

$$x=\frac{1}{2}\cdot at \cdot t$$

$$x=\frac{1}{2}at^2$$

となります．

初速度が0ではないときの等加速度直線運動

0秒の時の速度（初速度）が0ではない場合，\(v-t\)グラフは下のようになります．

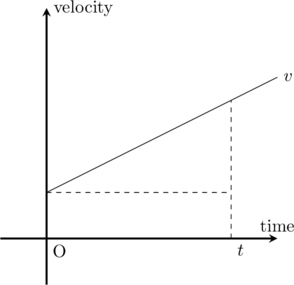
一見難しいように見えますが，初速度の分は等速直線運動と同じ長方形で，それを取っちゃえばさっきの等加速度直線運動で出てきた三角形と同じ形になるではありませんか！

つまり，初速度が0でない等加速度直線運動の場合は，等加速度運動で進む距離と初速度の分で進む距離とを別々に考えて足せばいいんです．

つまり，進む距離を\(x\)[m]，時間を\(t\)[s]，初速度を\(v_0\)[m/s]，加速度を\(a\)[m/s²]と置くと，式としては↓のようになります．

$$x=\displaystyle \frac {1}{2} at^2 + v_0 t$$

ちょっと混乱しているかもしれないので例題を使います．

例題1

加速度1[m/s²]で右向きに等加速度直線運動している物体がある．初速度が右向きに2[m/s]であったとき，この物体が5秒後に到達する距離\(x\)[m]を求めよ．

ただし，右向きを正，0秒の時の位置を0[m]とする．