みなさんこんにちは!今回は,投射系や速度を1つの公式で全部まかなう方法を紹介します!
投射系とは?
初速度を付けて物体を運動させること.初速度0の場合も一応投射の特殊な場合という捉え方で行きます.
初速度のある運動
- 等加速度直線運動
- 等速直線運動
- 鉛直投げ上げ
- 鉛直投げ下ろし
- 水平投射
- 斜方投射
初速度のない運動
- 自由落下
- 等加速度直線運動の一部
- 等速直線運動の一部
これらが全部一つの公式で済んでしまいます!
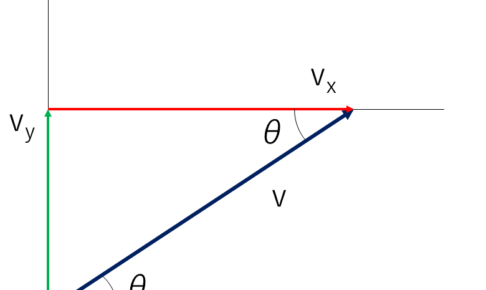
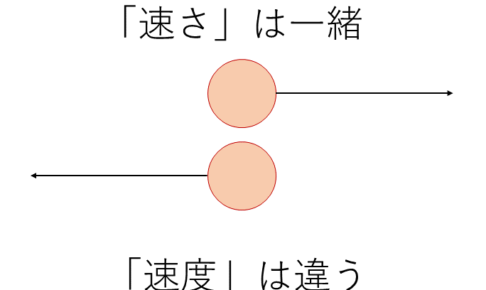
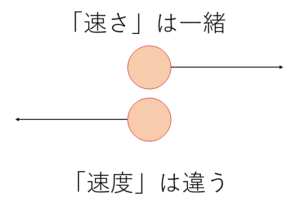
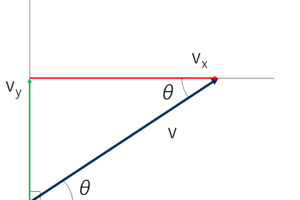
速度の分解
実際に速度や距離を求める時に「水平方向の速度と鉛直方向の速度」や「斜面方向の速度と斜面垂直方向の速度」に分けて考える必要があるので,まずは速度の分解を知る必要があります.
速度の分解のページをまだ読んでいない人はコチラ↓
公式紹介
本題の公式です!多分知っている人も多いはずのあの公式です.
$$x(またはy)=\displaystyle \frac{1}{2}at^2 +v_0t$$
\(x\):移動距離(変位)
\(y\):移動距離(変位)~\(x\)と垂直方向
\(a\):加速度
\(t\):経過時間
\(v_0\):初速度
この式の詳しい説明はコチラ↓
使い方

速度を
- 水平方向と鉛直方向
- 斜面方向と斜面垂直方向
のいずれかに分解します(大概この2つのどちらか).
分解の仕方が分からない方はコチラから↓
あとは分解した2つの方向それぞれにさっきの公式を当てはめるだけ.
たったのこれだけなんです.
とは言っても使い慣れないと難しいと思うので,例題を用意しました.
例題1(文字式がニガテな人向け)
[/su_spoiler]例題1(文字式Ver.)
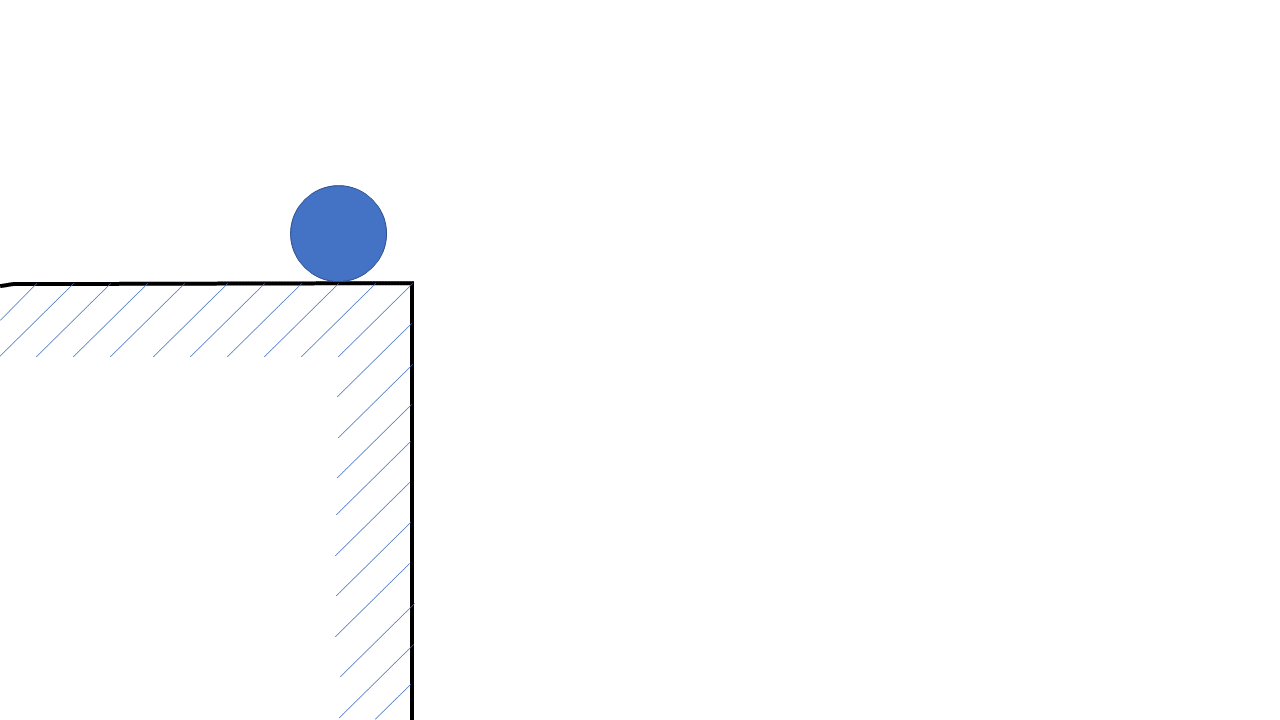
初速度\(v_0\)[m/s]で物体が右向きに水平投射されたとき,\(t\)[s]経過したときの物体の\(x\)方向の変位の大きさと\(y\)方向の変位の大きさを求めよ.
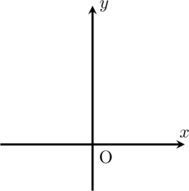
物体が水平投射運動を始めた点を原点とし,重力加速度を\(g\)[m/s2],座標軸の方向を下の図のように取るものとする.



コメントを残す