半減期～混乱しないで計算式を立てる方法

半減期

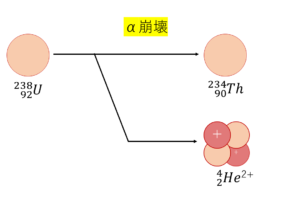
半減期とは，原子核が崩壊していく過程で，崩壊しないで残っている原子の割合が半分になるまでにかかる時間のことを言います．

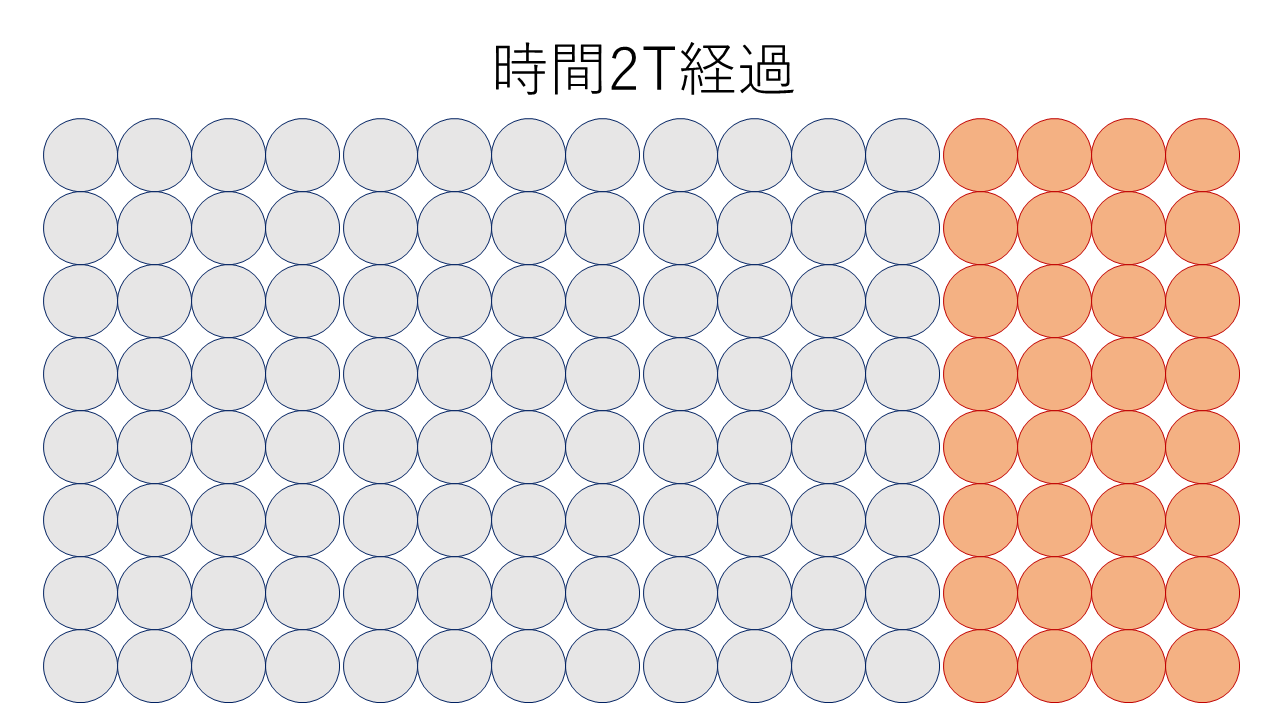
半減期事に半減していく元の原子核のイメージを作ってみました．本来であれば崩壊していく原子核は均等に分布しているので，こんなきれいにはなりません．あくまでイメージです．

半減期をT，元の原子核がオレンジ，崩壊した原子核が灰色で表してあります．

半減期ごとに元の原子核が半分になっているのが分かると思います．

じゃあ，半減期ちょっきりじゃないときは，どれくらい元の原子核が残っているかってどうやって計算するのでしょうか．

今回は暗記ではなく，式を立てて導出するやり方を授けます．

経過時間と半減期から式を立てる

まず，問題に与えられているかどうかを一切無視しましょう．それから，問題で何を求めるかも一切無視．

全部無視して自分の中で1度組み立ててしまうのが混乱防止のポイントです．

手順はこんな感じ↓

1. 自分で必要な物を文字で置く（日本語でおいてもいいけど時間かかる）
2. 等式を組み立てる
3. 問題文で与えられているものと比較して，代入したり文字を変えたりする

正しい文字じゃなくても全然大丈夫．一般的には，最初に存在する原子の個数を\(N_0\)とかっておきますが，知らなかったら\(x_0\)とかって適当に置いちゃいましょう．

今回必要なのは，

• 元の原子核の数\(N_0\)
• 原子核の半減期\(T\)
• 経過時間\(t\)
• 時間\(t\)の時の元の原子核の数

この4つ．

物理は必要な物を見つけてくることが結構大事なので，これは訓練しておきましょう．

あとは等式を立てます．元の原子核の数は，半減期1回分で\(\displaystyle \frac{1}{2}\)，半減期2回分で\(\displaystyle \frac{1}{4}\)になる→つまり，半減期何回分かっていうのがポイントになってきそうですね？

時間\(t\)の間に何回元の原子核の量が\(\displaystyle \frac{1}{2}\)になったかってことです．半減期は\(T\)なので，時間\(t\)の間に\(\displaystyle \frac{t}{T}\)回元の原子核が半分になったということです．

ってことは，初期段階での元の原子核の数が\(N_0\)，時間\(t\)後の元の原子核の数が\(N\)，半分になった回数(\displaystyle \frac{t}{T}\)回なので，これを等式で置くと，

$$N=N_0 \times \left( \frac{ 1 }{ 2 } \right) ^{\frac{t}{T}}$$

になります．あとは問題で与えられた文字に代えたり，求めたいものについて方程式を解くだけ．計算がニガテな私にとっては方程式を解くのが結構ツライのですが…

きっと物理ができなくて困っている人は，そもそも式が立てれないという人がほとんどだと思います．

今回のようにとにかく問題の記号を無視し（できれば問題の記号で一発でできるのが理想だけど），自分の文字ルールを作ってそこで考えてみてください．

そうすると，自分で決めたルールに従っているので頭が混乱せずに済みます．「あれ？経過時間ってなんの文字で置いてたっけ？？」と問題文を振り返る時間も無くなります．

以上，半減期の計算でした