ボーアの理論

今回は，エネルギー準位とボーアの理論です．

電荷を持つ粒子は，円運動など加速度を受ける運動をすると電磁波を放出してエネルギーを失っていくことが知られています．

この現象に従うと，ラザフォードの原子模型の電子は軌道を保てず勝手に原子核に落っこちていってしまい，原子が崩壊してしまいます．しかも電子が落っこちていくときに放出する電磁波は連続した波長をもつはずなのに，観測されたのは飛び飛びの波長をもつ線スペクトル．

なんで観測される波長は飛び飛びなのか，さらに原子は崩壊しないで済むのか．その問いに対して明確な理論を提唱したのが今回の「ボーアの理論」．

ボーアの理論は，

量子条件
振動数条件

の2つの条件で成り立っています．

量子条件

本来の量子条件は，角運動量というものを量子化する意味があります．しかし，高校では角運動量をやらないので，今回は下の「補足」にまとめてあります．

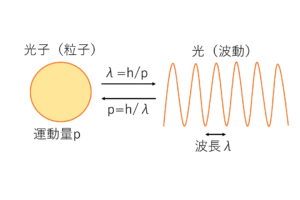
高校で理解しなくてはならないのは，「電子が存在できる軌道は，電子の波長の整数倍の長さを持つ軌道だけ」ってこと．

これを式にしたのが量子条件．

$$量子条件$$

$$2πr=nλ$$

電子がこの軌道上にある時のことを「定常状態」と呼びます．また，定常状態にある電子が持つエネルギーのことを「エネルギー準位」と呼びます．

定常状態では，電子が物質波だと捉えた時の波（電子波）が干渉しない状態を保てます．一方，軌道長が電子の波長の整数倍にならないときは，波が干渉を起こして打ち消されるので，整数倍にならない軌道には電子が存在できないことになります．

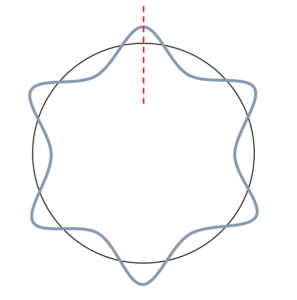
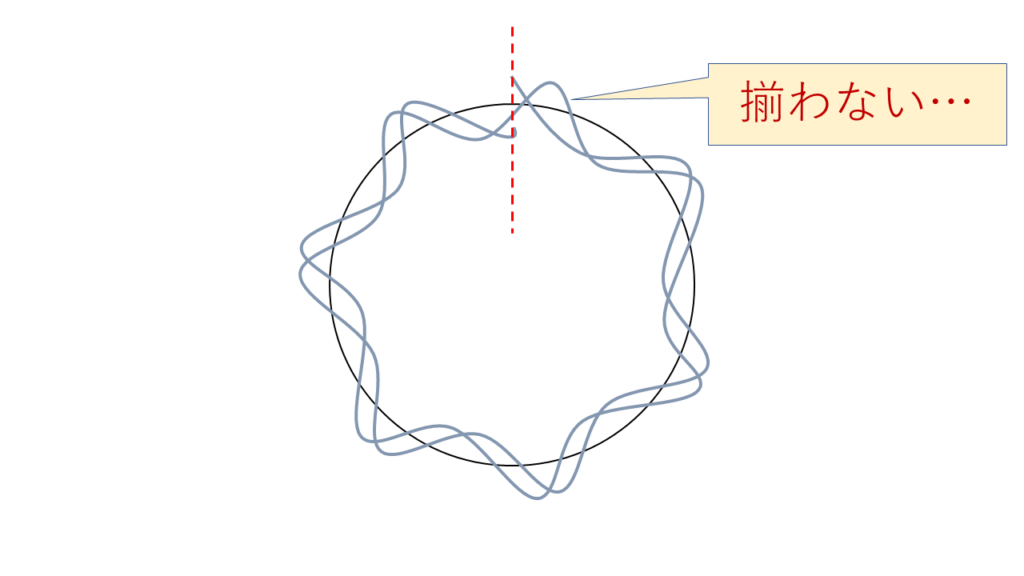
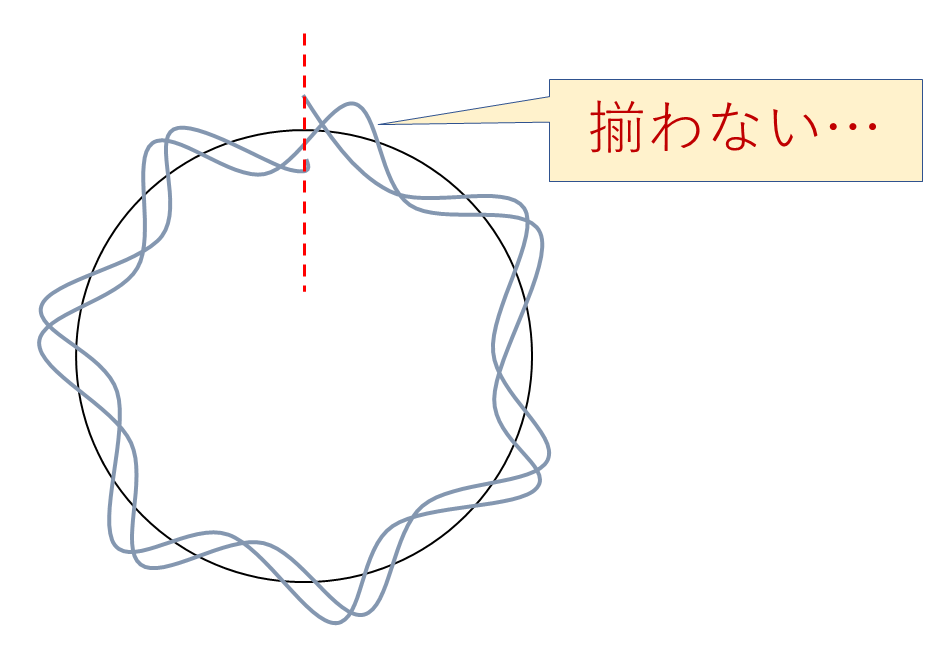
下の画像は，定常状態と非定常状態の時の波長と軌道長を図にしたものです．

円が軌道，波で表されているほうが波長です．山一つ分で1波長になります．

定常状態（n=6)↓

非定常状態(n=5.7)↓

補足

実際の量子条件は，角運動量という概念を用います．角運動量とは，通常の運動量に回転半径$r$をかけたもので，円運動における運動量的な立ち位置にあります．

運動量・速度・加速度がセットで出てきますが，角運動量は，角速度・角加速度とセットで出てくるものです．

角運動量を用いた本当の量子条件は，

$$mvr=n \cdot \frac{h}{2π}(n=自然数)$$

と表されます．これは，角運動量が量子化されたことを意味していて，ここにドブロイ波長を導入することで，電子の軌道が，電子波の波長によって表現できるのです．

$$\begin{eqnarray}\left\{\begin{array}{l}
λ=\displaystyle \frac{h}{mv} \\
mvr=n \cdot \displaystyle \frac{h}{2π}(n=自然数)
\end{array}
\right.
\end{eqnarray}$$

$v$を消去するために，$v=\displaystyle \frac{h}{mλ}$と変形して代入します．

$$m \cdot \frac{h}{mλ}r=n \cdot \displaystyle \frac{h}{2π}(n=自然数)$$

$2πr$について解くと，

$$2πr=nλ$$

となり，軌道長が波長の自然数倍になることが示されました．

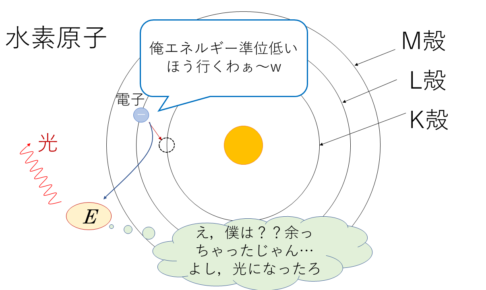
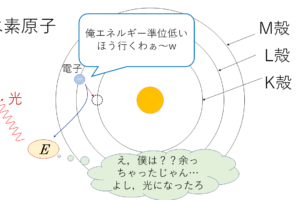
振動数条件

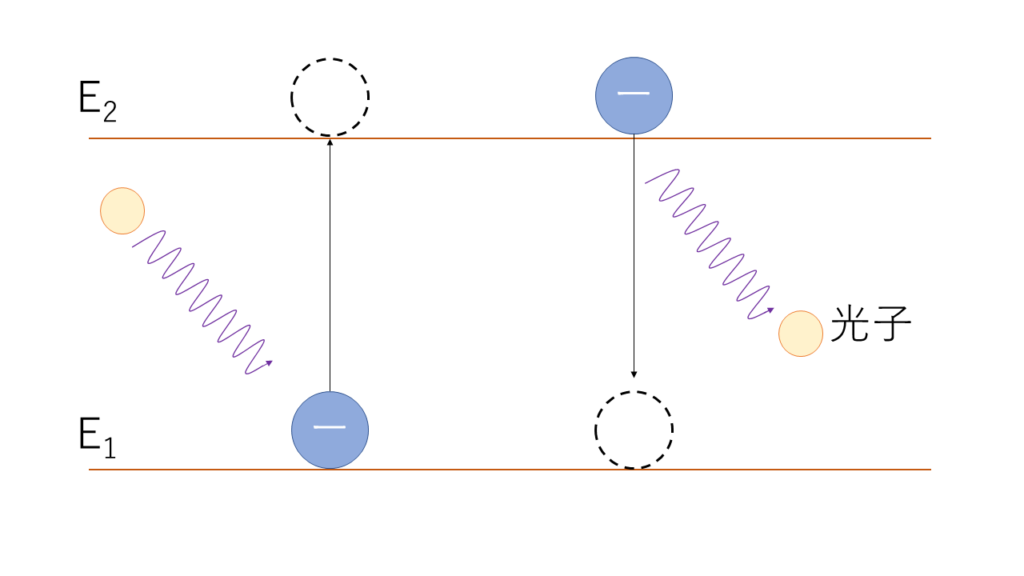
これはスペクトルの章でも説明してしまいましたが，ざっくり言うと，電子が別の軌道に移るとき，エネルギーの過剰分や不足分は光として放出・九州されるというものです．

移動先でのエネルギー準位のほうが高ければ光子のエネルギーを吸収，移動先のほうが低ければ光子を放出します．

下の図は，エネルギー準位E₁とE₂を電子が移動するときのイメージ図です（E₁<E₂)

その時，吸収・放出するエネルギーの大きさは，

$$E=hν$$

で表されます．

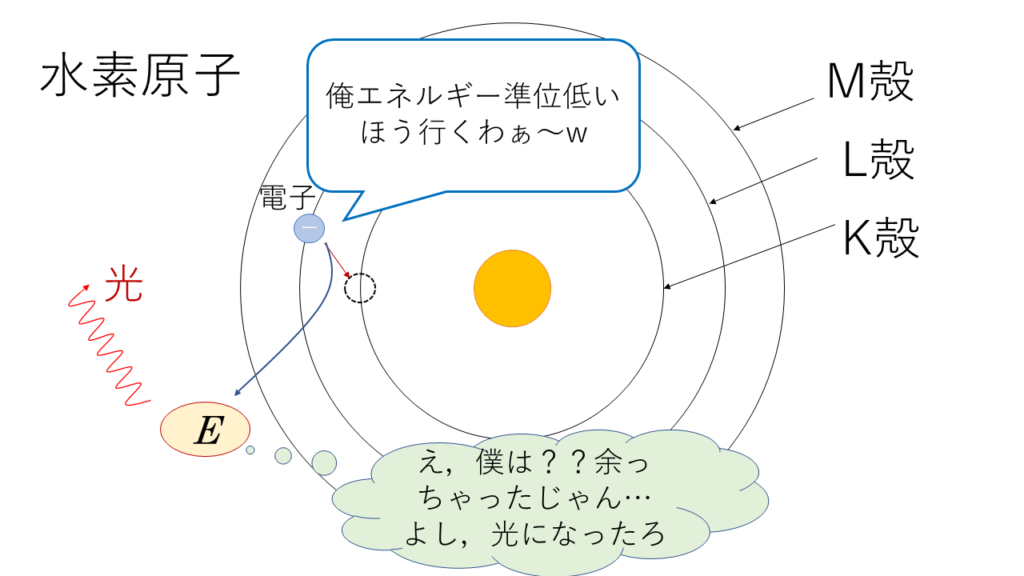
イメージはこんな感じ．今回は放出されるパターンです．

スペクトルのほうでも同様の説明をしていますので，読み返してみてください↓

スペクトル

2020年4月23日

エネルギー準位の計算

電子が速度$v$で等速円運動していると仮定すると，クーロン力による向心力と，遠心力が釣り合うので，

$m$:電子の質量
$r$:半径
$k_0$:真空でのクーロン力比例定数
$e$

$$\frac{mv^2}{r}=k_0\frac{e^2}{r^2} \tag{1}$$

が成立する．

量子条件とドブロイ波長より，

$$2πr=\frac {h}{mv}\cdot n (n=自然数)$$

$$v=\frac {h}{2πmr} \cdot n$$

両辺を二乗して，

$$v^2=\frac {h^2}{4π^2 m^2 r^2} \cdot n^2$$

これを式(1)に代入すると，

$$\displaystyle \frac{m \displaystyle \frac {h^2}{4π^2 m^2 r^2} \cdot n^2}{r}=k_0\frac{e^2}{r^2}$$

$r$について整理すると，

計算省略

$$\displaystyle \frac{m h^2}{4π^2 m^2 r^3} \cdot n^2=k_0\frac{e^2}{r^2}$$

$$\displaystyle \frac{h^2}{4π^2 mr} \cdot n^2=k_0e^2$$

$$r=\displaystyle \frac{h^2}{4π^2k_0me^2} \cdot n^2 (n=自然数) \tag{2}$$

という式が成り立ちます．

これを直接使うわけではなくて，これを使ってさらにエネルギーの総和を求めていきます．

電子の持つエネルギーの総和は，位置エネルギーと運動エネルギーの和になります．

$$E=U+K \tag{3}$$

万有引力の時にもやったと思いますが，位置エネルギーの基準点を無限遠に置くと，位置エネルギーは

$$U=-k_0 \frac{e^2}{r} \tag{4}$$

運動エネルギーはご存じの

$$K=\frac{1}{2}mv^2$$

これと，運動方程式（遠心力と向心力のつり合い式）

$$m\frac{v^2}{r}=k_0 \frac{e^2}{r^2}$$

を変形した式

$$mv^2=k_0 \frac{e^2}{r}$$

より，運動エネルギー$K$は，

$$K=k_0 \frac{e^2}{2r} \tag{5}$$

と変形されます．

式(3),(4),(5)より，電子の持つエネルギーの総和は，

$$E=-k_0 \frac{e^2}{r}+k_0 \frac{e^2}{2r}$$

$$=-k_0 \frac{e^2}{2r}$$

となります．上の式の$r$に先ほど計算した式(2)を代入すると，

計算省略

\begin{eqnarray}
\left\{
\begin{array}{l}
E=-k_0 \frac{e^2}{2r}\\
r=\displaystyle \frac{h^2}{4π^2k_0me^2} \cdot n^2 (n=自然数)\end{array}
\right.
\end{eqnarray}

$$E_n=-k_0\frac{e^2}{2}\cdot \frac{4π^2k_0 me^2}{h^2}\cdot \frac{1}{n^2}$$

$$E_n=- \displaystyle \frac{2πk_0^2 me^4}{h^2} \cdot \frac{1}{n^2} (n=自然数)$$

となります．

nが1の時，エネルギー準位は最低になります．この時のエネルギー準位を「基底状態」，nが1以外の自然数の場合を「励起状態」と呼びます．

通常の状態では，原子内の電子は常に基底状態を取っていますが，光子がぶつかって励起されると，エネルギー準位の高い軌道に移ります．これが励起状態．

エネルギーの高い軌道にどんどんと移動し，最終的にnが無限大，つまり軌道半径$r$も無限大を取る時，その電子は原子外に放出されます．

原子外に放出されるということは，原子がイオン化されるということです．

この時のエネルギーが「イオン化エネルギー」と呼ばれています．基底状態の電子を励起させて原子の外に放出するために必要なエネルギーがイオン化エネルギーの正体だったのです．化学とつながった感じがするでしょ？？

というわけで，今回はボーアの理論とエネルギー準位についてでした．