ミリカンの油滴実験・電気素量

今回は，ミリカンが行った電気素量を求める実験です．

電気素量とは？

電気素量は，ざっくりと「電子1粒が持つ電気量(電荷の大きさ)」って覚えて大丈夫です．

もちろん陽子1粒が持つ電荷の大きさも電気素量です．

それを求めようとしたのが今回の実験．

ミリカンの実験装置

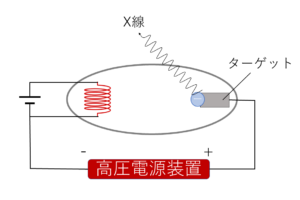
絶縁体の容器の中に極板を入れて，X線を使って空気をイオン化させます．そのイオンが油滴に付着することによって油滴は帯電し，極板間に作られた電場の影響を受けるようになります．

油滴が静止しているとき，重力と静電気力が釣り合っているという等式を立てることができ，さらに電場を与えずに油滴が等速直線運動をしているとき，重力と空気抵抗が釣り合っているという等式が立ちます．

この2つを連立して電荷の大きさ\(q\)を出して，その数値の法則性を見つけようとしたのが今回の実験です．

実験

油滴に帯電した電荷と，極板によって作り出される電場によって，重力に抵抗する静電気力が発生します．

帯電した電荷の大きさを\(q\)，加えた電場の大きさを\(E\)，重力加速度を\(g\)，油滴の質量を\(m\)とします．

重力と静電気力が釣り合って油滴が静止しているとき，

$$mg=qE \tag{1}$$

であり，油滴が落下していくと，空気抵抗によって終端速度に達します．

空気抵抗は速度に比例するので，比例定数を\(k\)，速度を\(v\)と置くと，

$$mg=kv \tag{2}$$

となります．

(1)，(2)式を連立すると，

$$kv=qE$$

$$q= \frac{kv}{E}$$

となり，質量\(m\)に依存しない形が出来上がります．

これをミリカンは何度も行い，電荷の大きさ\(q\)が常に約1.592×10^-19[C]の整数倍になることを発見しました．

これが電子一つが持つ電荷の大きさで，電気素量の正体です．

現在は，\(e=1.60217653×10^-19\)[C]が正確な電気素量です．

電気素量まとめ

電気素量について試験にでがちなポイント・押えておくべきポイントをまとめました．

• 電気素量を表す記号は\(e\)，単位はクーロン[C]
• \(e \simeq 1.6 \times 10^-19\)[C]←暗記しておいたほうがよき
• 電気素量よりも小さな電気量は基本的には存在しない

電気素量・例題

ミリカンの実験でいくつかの油滴の電気量を測定した．以下にその結果を示す．

$$3.2  11.3   9.5  12.6  6.3 [10^-19C]$$

油滴に帯電した電気量は電気素量の整数倍だと仮定して，電気素量\(e\)を求めよ．有効数字は三桁とする．

以上，ミリカンの油滴実験と電気素量でした．