コンプトン効果・コンプトン散乱

今回のテーマはコンプトン効果についてですがぶっちゃけコンプトン効果で大切なのは「光子の持つ運動エネルギー」だけです．X線光子が電子に衝突する過程と，それに伴うエネルギーと運動量の変化を見ていきますが，暗記するのは光子の運動量だけで十分．

コンプトン効果

コンプトン効果とは，超ざっくりいえばX線が電子などに衝突して散乱する際，ぶつかる前と後では波長が異なる現象です

X線ではなく可視光の場合，物体に可視光が当たっても波長（光の色）は変化しないように見えますよね？ぶつかった後も波長は変化しないのが波の特徴なのです．しかし，X線を物質にぶつけ散乱させたとき，ぶつかった後に波長が変化してしまう現象が発見されました．これがコンプトン効果です．

X線が波であるなら物質と衝突しても衝突前後で波長は変わらないのですが，コンプトン効果が発見され，衝突前後の波長が違うという事実が明らかになったことにより，X線は波動として考えると理論上おかしくなってしまいます．

そこで提案されたのが，アインシュタインが発案した「光子の運動量」という考え方．

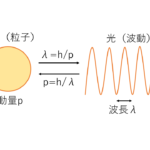
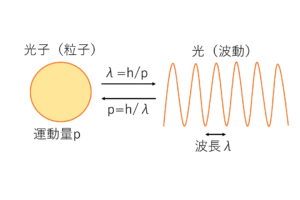
アインシュタインは，光が「光子」という粒子で構成されていると捉えた上で，光子のエネルギー\(E=hν\)とともに下のような運動量\(p\)を持つと考えました．

$$p=\frac {hν}{c}=\frac{h}{λ}$$

$$運動量=\frac{プランク定数\dot振動数}{光速}$$

$$=\frac{プランク定数}{波長}$$

単位：\(p\)[kg・m/s]　光子の運動量

\(h\)[J・s]　プランク定数

\(ν\)[Hz]　光の振動数

\(c\)[m/s]　光速

\(λ\)[m]　波長

アインシュタインは，光が粒子であるという仮定から，光子はエネルギーと運動量を持ち，エネルギーと運動量はそれぞれ保存されるという結論を導きました．

コンプトン効果の実験

この実験は，「そんなことやったんだ～へぇ～」くらいの理解で十分です．計算量多いので要注意．

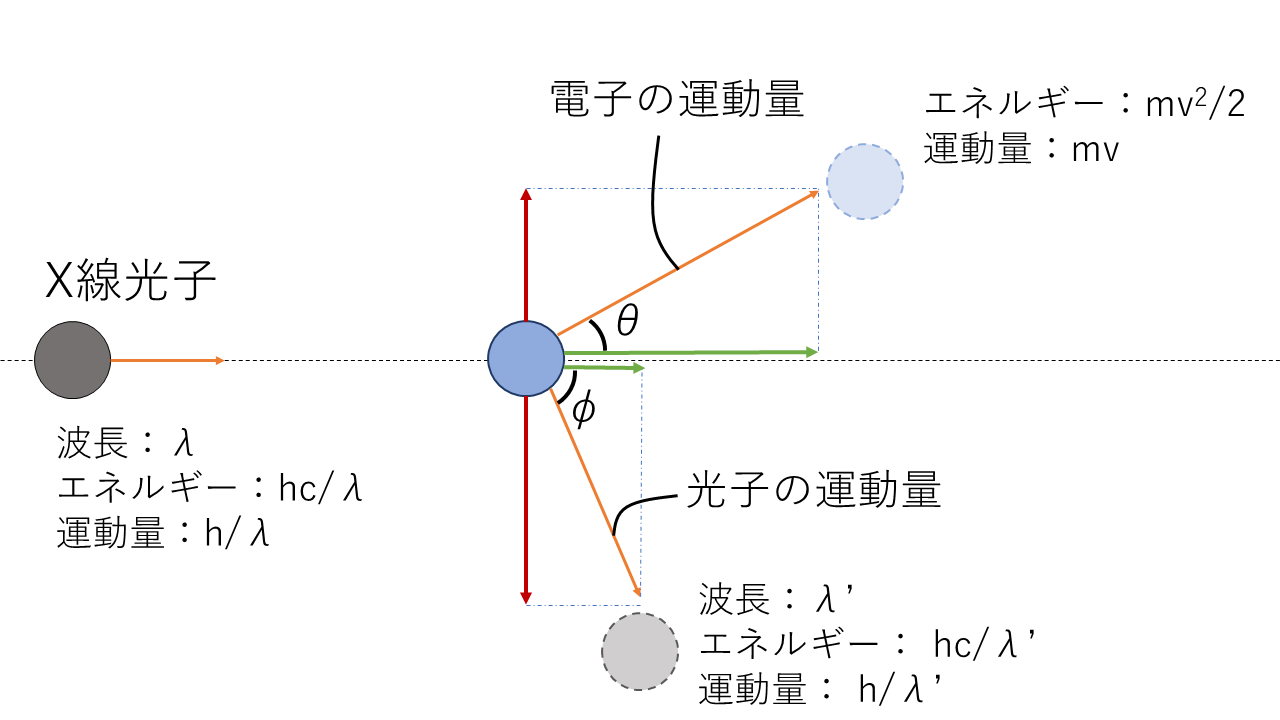
コンプトン氏は，アインシュタインの光子論に基づき，X線を電子に当てて散乱させ，衝突後の電子とX線のエネルギーや運動量の変化を調べる実験を行いました．

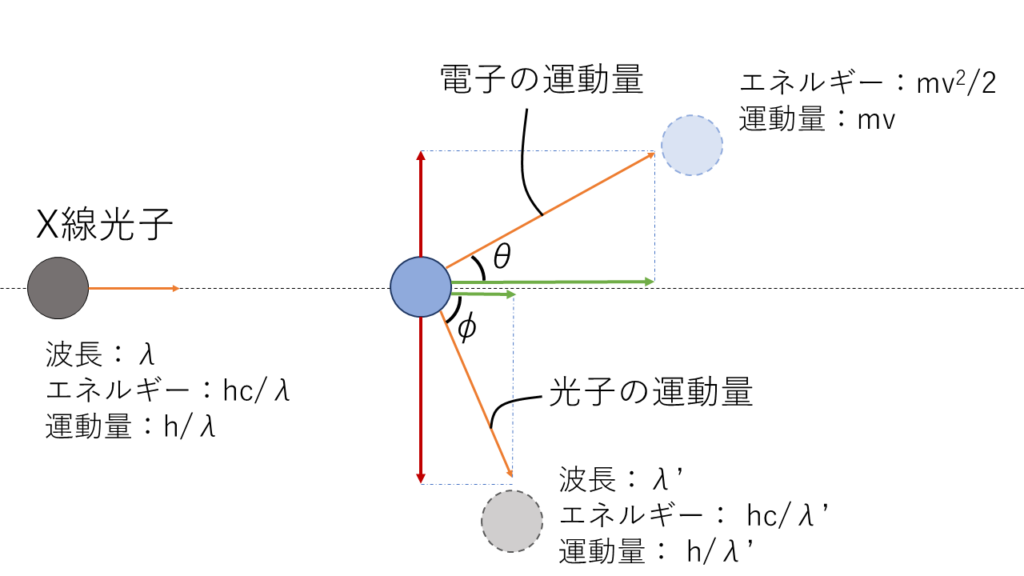
これが運動量保存則とエネルギー保存則に基づいていると仮定して話を進めます．

まず，エネルギーの保存から式を立てると，

$$\frac{hc}{λ}=\frac{hc}{λ’}+\frac{1}{2}mv^2 \tag{1}$$

水平方向の運動量保存から式を立てると，

$$\frac{h}{λ}=\frac{h}{λ’}\cos φ+mv\cos θ\tag{2}$$

同様に，鉛直方向で式を立てると，

$$0=\frac{h}{λ’}\sin φ-mv\sin θ \tag {3}$$

(1),(2)式を変形して，それぞれ

$$mv\cos θ=\cos φ\frac{h}{λ}-\frac{h}{λ’} \tag{4}$$

$$mv\sin θ =\frac{h}{λ’}\sin φ \tag{5}$$

(4),(5)式をそれぞれ2乗して，各辺を足し合わせると，

$$(mv)^2=(\frac{h}{λ}-\frac{h}{λ’}\cos φ )^2+(\frac{h}{λ’}\sin φ)^2$$

右辺を整理して，

$$(mv)^2=h^2(\frac{1}{λ^2}-\frac{2}{λλ’} \cos φ+\frac{1}{λ’^2})$$

続いて(1)式の両辺に\(2m\)をかけて，

$$(mv)^2=2mhc(\frac{1}{λ}-\frac{1}{λ’})$$

を作ります．

これを先ほどの\((mv)^2\)に代入して，

$$2mhc(\frac{1}{λ}-\frac{1}{λ’})=h^2(\frac{1}{λ^2}-\frac{2}{λλ’} \cos φ+\frac{1}{λ’^2})$$

両辺に\(\displaystyle \frac{λλ’}{2mch}\)をかけて整理すると，

$$λ’-λ=\frac{h}{2mc}\cdot (\frac{λ’}{λ}+\frac{λ}{λ’}-2\cos φ)$$

ここで，\(λ　\simeq λ’\)と近似すると，

\(\displaystyle \frac{λ’}{λ}+\displaystyle \frac{λ}{λ’}\sineq 2\)と近似できるので，

$$λ’-λ=\frac{h}{mc}\cdot (1-\cos φ)$$を得る．