本来,光が波の性質をもつというのは「波動」の単元で学習したと思います.
事実,光は電場と磁場が垂直に振動する波の現象であることは間違いありません.
ですが,光が波だという理論に従うと説明がつかない現象が発見されたのです.それが光電効果やコンプトン効果です.
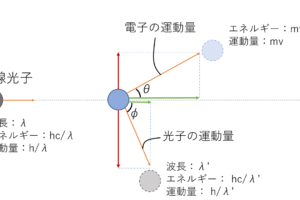
コンプトン効果はX線の章で解説しています.
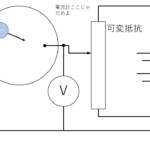
今回の標的はズバリ,この光電効果の実験.
光量子説
光量子説は,かの有名なアインシュタインが提唱した説.
光を粒子の流れとしてとらえ,その本来,光が波の性質をもつというのは「波動」の単元で学習したと思います.
事実,光は電場と磁場が垂直に振動する波の現象であることは間違いありません.
ですが,光が波だという理論に従うと説明がつかない現象が発見されたのです.それが光電効果やコンプトン効果です.
コンプトン効果はX線の章で解説しています.
今回の標的はズバリ,この光電効果の実験.
光量子説
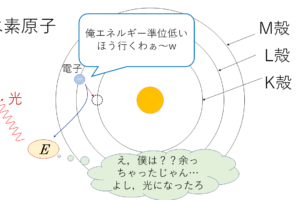
光量子説は,かの有名なアインシュタインが提唱した説.光を粒子としてとらえたのです.この粒子のことを光子(光量子)と呼びます.
光を波ではなく光子の流れととらえ(電流みたいなイメージです),光子一つ一つは振動しており,エネルギーを持っているという考えを提唱しました.
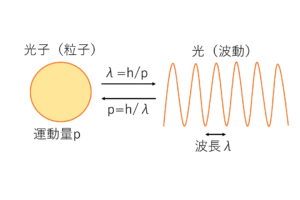
この時の光子ひとつがもつエネルギーを,光子の振動数\(ν\)[hz]としたときに次のようなエネルギーを持つと提唱しました.
$$E=hν=\frac{hc}{λ}$$
$$光子のエネルギー=プランク定数\times光子の振動数=\frac{プランク定数\times 光の速度}{光の波長}$$
単位:E[J] 光子のエネルギー
\(h\)[J \cdot s] プランク定数
\(ν\)[Hz] 光の振動数
\(c\)[m/s] 光の速さ(真空中)
\(λ\)[m] 光の波長
光電効果と仕事関数
金属の表面に光を当てると,そこから電子が飛び出してくる現象のことを光電効果と呼びます.
この時飛び出してくる電子のことを光電子と呼んでいます.
光電効果の大きな特徴をまとめてみました.
- どんなに強い光でも,光が一定の振動数を超えないと光電子は飛び出してこない.逆に,一定の振動数さえ超えれば弱い光でも光電子は飛び出す.この境目になっている振動数のことを,限界振動数\(ν_0\)[Hz]と呼ぶ.
- 飛び出した光電子の運動エネルギーの最大値は,当てた光の振動数に依存する.
- 振動数が一定の光だと,光の強さが強くなっても運動エネルギーの最大値は変化しない.飛び出してくる光電子の数は増える.
特に3番が試験問題に利用されやすい特徴.
仕事関数とは?
金属原子から光電子を放出するために必要な最低限のエネルギー(仕事)のこと.「関数」という名前がついているからと言って何かの関数になっているわけではなく,ただの数値です.一般に記号は\(W\),単位は[J].
金属内では,自由電子が原子核からの引力(静電気力)を受けています.この自由電子が「光電子」として飛び出すわけですが,そのためには原子核からの引力を振り切る必要があります.この時に必要な仕事の量が仕事関数って命名されたわけなのです.
光電子が飛び出すときに,電子は光子のエネルギーすべてを受け取りますが,エネルギーの一部は仕事関数として消費されてしまい,残った分が運動エネルギーとして現れます.
つまり,飛び出してくる光電子の運動エネルギーのうち最大のものは,光子のエネルギーから仕事関数を引いたものになります.
こうして無事に飛び出してきた光電子のうち最大の運動エネルギーを一般に\(K_0\)としています.
ここまで解説してきたことを式でまとめると以下のようになります.
$$K_0=hν-W$$
$$運動エネルギー(最大)=光子のエネルギー-仕事関数$$
$$E=hν=\frac{hc}{λ}$$
$$光子のエネルギー=プランク定数\times 光の周波数=\frac {プランク定数 \times 光速}{波長}$$

コメントを残す