核分裂・核融合～どっからエネルギー来てるん？？

こんにちは！今回は核分裂と核融合のお話．あの原子爆弾がなぜあんなに大きなエネルギーを取り出せるのか，その根本は理解できるようになります．

今回の理論はアインシュタインが考案したので，このページを読み終えた頃には，あの偉大なアインシュタインにちょっと近づいているでしょう．

核反応（原子核反応）

核反応は，化学でいう所の「化学反応」みたいな感じのイメージです．化学反応の場合には，原子核は一切変化しません．しかし，今回の核反応は原子核の変化を扱う反応です．

核反応のイメージが掴みにくいと思うので，とりあえず一例を．

$${}^{14}_7 N +{}^4_2 He → {}^{17}_8 O +{}^1_1 H $$

これが核反応式です．

原子の組み合わせが変わったわけではなく，原子核そのものが変わってしまっているのが分かると思います．

原子の組み合わせではなく，原子核を構成している「陽子」や「中性子」の組み合わせが変わっているのが最大の特徴．

これさえ押さえれば核反応式の意味は十分理解できたと思います．

核反応は粒子と粒子が衝突して原子核が変化する反応のことなので，放射性崩壊とかはちょっと別物になります．

化学反応式やイオン反応式では，各原子の数や電気量が反応前と反応後で保存されていました（反応前と反応後で不変）が，核反応式でも同じような現象が起きます．

核反応式では，原子番号の和と質量数の和が保存されます．他にも原子番号の和=陽子の数の和ということもできるので，電気量の和が保存されるという言い方もできます．

さっきの

$${}^{14}_7 N +{}^4_2 He → {}^{17}_8 O +{}^1_1 H $$

の式でいうなら，元素記号の左下にある数字の和，左上にある数字の和は，それぞれ左辺と右辺で等しいっていうこと．核反応式の場合はこれを使って左辺と右辺の数合わせをするだけです．

質量とエネルギーの関係（等価性）

実は質量とエネルギーは同等で，質量をエネルギーに換算することができます．その式がコチラ↓

$$E=mc^2[J]$$

$E$：エネルギー[J] $m$：質量[kg] $c$：光速（真空中)[m/s²]

$m$も$c$もよく出てくるので，日本語で式を覚えなくても，$E=mc^2$のリズムで覚えてしまいましょう．

質量が大きい物質ほど，より大きなエネルギーを持ちます．また，質量が軽くなったときは，質量の差がエネルギーとしてどこかに放出されることになります．

質量欠損・原子核の結合エネルギー

化学の「結合エネルギー」ならイメージしやすいと思うので，結合エネルギーと対比して説明していきます．

化学の結合エネルギーの復習

化学の結合エネルギーは，分子の状態の気体を原子単体に分ける時に必要なエネルギーの大きさでした．

H-Hの結合エネルギーは，くっついている状態のH原子とH原子を引き剥がしてH原子単体にするために必要なエネルギーのことでしたよね？

C-Hの結合エネルギーも同様に，CとHがペアになっているのを引き剥がしてC原子とH原子に分けるために必要なエネルギーのことでした．

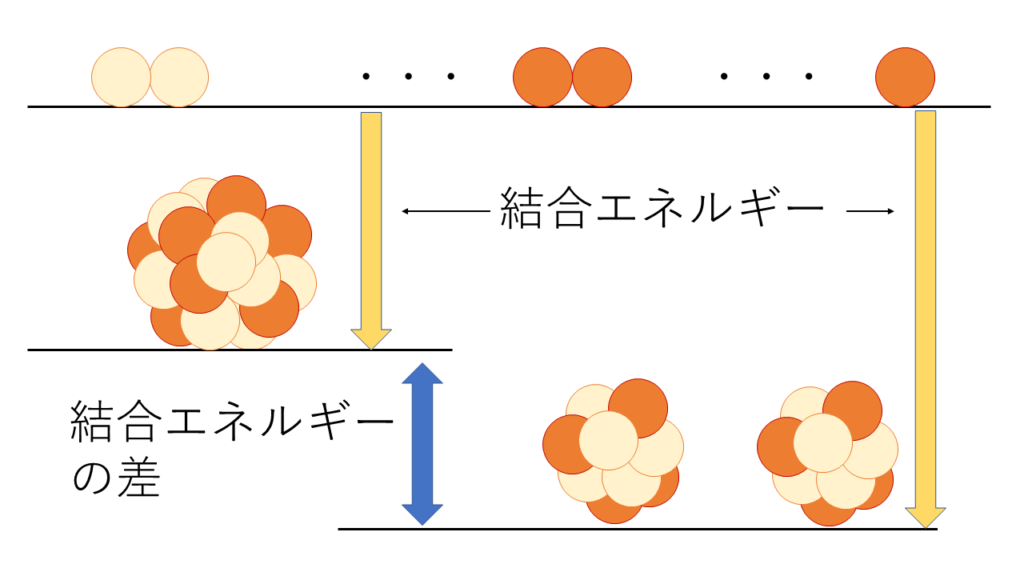
化学の結合エネルギーの場合はペアになっている原子同士を分けるためのエネルギーでしたが，原子核の場合は，原子核内の陽子と中性子をすべてバラバラの状態にするのに必要なエネルギーのことです．

原子核の結合エネルギーが大きい原子ほど，持っているエネルギーが低いので，より安定な状態になります．

陽子と中性子を，バラバラで存在している状態から原子核を形成している状態にすると，バラバラの状態よりも原子核になった状態のほうが質量が軽くなります．この軽くなった分を「質量欠損」と呼びます．

先ほどの「質量がエネルギーに換算できる」という知識を使うと，原子核を形成したことによって発生した質量欠損は，失った質量分のエネルギーを放出したことになります．

核エネルギー

核反応の前と後では，原子核の質量の和が変化しています．

反応前の原子核の質量の和と比べて反応後の質量の和が減少していたとき，反応前後の質量和の差に相当するエネルギーのことを「核エネルギー」と呼びます．

※質量和の差ってややこしいですよね．核反応では2つ以上の原子核や中性子によって反応するので，反応前の原子核や中性子の質量和と，反応後の質量和を比べるわけです．

反応前後の質量の差って言ったほうが人によっては分かりやすいかもしれません．

核分裂反応

さていよいよみなさんおなじみの核分裂です．

核分裂は，原子力発電や原子爆弾にも使わている反応で，これを読んだらどうしてあんなに大きなエネルギーが取り出せるのかがわかります．練習問題もつけてありますので，問題を解いて核分裂によって取り出せるエネルギーがどれだけすごいものなのかを体感してみてください．

核分裂は，一つの原子核が複数の原子核に分裂する反応のこと．

結合エネルギーは鉄56あたりで最大になる=鉄56あたりが一番安定した原子核なので，これよりも質量数の大きい原子核は，崩壊して2つの原子核になったほうが安定します．

核分裂を起こりやすくするために，分裂させる原子核に中性子を当てて分裂させます．

この時，分裂して発生した原子核・中性子の質量和は，元の原子核・中性子の質量和に比べて小さくなります．（鉄56より質量数の大きな原子核が分裂した場合）

必ずしも核分裂後は質量が軽くなるわけではない

結合エネルギーは，鉄56あたりで最大値を取ります．つまり，鉄56あたりが一番エネルギーの低く安定した状態っていうことです．

鉄の原子核を核分裂させる場合は，分裂後の原子核のほうが質量和が大きいので，分裂時にエネルギーを吸収しなければなりません．なので，普通は分裂後の質量和が分裂前より重くなる核分裂は起こりません．

つまり，質量を失っているわけです．

質量を失ったということは，質量相当分のエネルギーを失っていることになります．

失ったエネルギーは$ΔE=Δmc^2$の$Δm$に失った質量を代入して計算することができます．

例題

次の核反応式の空所$x$に当てはまる数字を求め，この反応で生じるエネルギー$E$[J]を求めよ．

$${}^{235}_{92}U + {}^1_0 n→{}^{92}_{36} Kr + {}^{141}_{56} Ba + x {}^1_0 n$$

${}^{235}_{92} U，{}^{92}_{36} Kr，{}^{141}_{56} Ba，{}^1_0 n $の質量をそれぞれ234.9935[u],91.9064[u],140.8837[u],1.0087[u]，真空中の光の速度$c=3.00 \times 10^8$[m/s]，1u$=1.66 \times 10^{-27}$[kg]とする．

解答

質量数（原子核内の中性子や陽子の数）は保存されるので，質量数について方程式を立てると，

$$235+1=92+141+ 1 \times x$$

$x$について方程式を解くと，

$$x=3$$

続いて，質量の減少分を求めます．

反応前の質量和は

234.9935+1.0087=236.0022[u]

反応後の質量和は

91.9064+140.8837+1.0087×3=235.8162[u]

よって質量差は，

=0.186[u]

になり，これをkgに直すと，真空中の光の速度$c=3.00 \times 10^8$[m/s]，1u$=1.66 \times 10^{-27}$[kg]より，

$$E=0.186[u] \times (1.66 \times 10^{-27}) \times (3.00 \times 10^8)^2$$

$$E \simeq 2.77 \times 10^{-11}[J]$$

となります．

ウラン235が1mol（235g）あった時，単純に答えのエネルギーを$6.0 \times 10^{23}$すればいいわけです．計算してみたらわかりますが，すごい数字になったと思います．だいたい$1.66 \times 10^12$[J]くらいです．それだけ核反応で得られるエネルギーは化学反応（燃焼）の比ではないのです．

これが原子力発電や原子爆弾で大きなエネルギーを生み出せる理由．

※ウランが核燃料として使用されるときは，3%濃縮くらいのウランを使用しますので，こんな単純な話ではなく，発生するエネルギーは先ほどの3%程度になります．それでも発生するエネルギーは$4.98\times 10^{10}$[J]くらい．

灯油0.3L分（235g相当）を燃焼させたときに発生する熱量はだいたい$1.1 \times 10^{7}$[J]くらいなので，それと比べてどれだけ莫大なエネルギーを発生させているかがわかると思います．