光電効果の実験として用いられることの多い光電管の実験です.
光電管
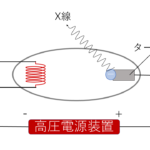
構造はこんな感じ.
内部を真空にしたガラス管に2つの電極を設置し,片方の電極に金属板を付けます.この金属板に光を当てることによって光電子が飛び出します.
実験装置を組む
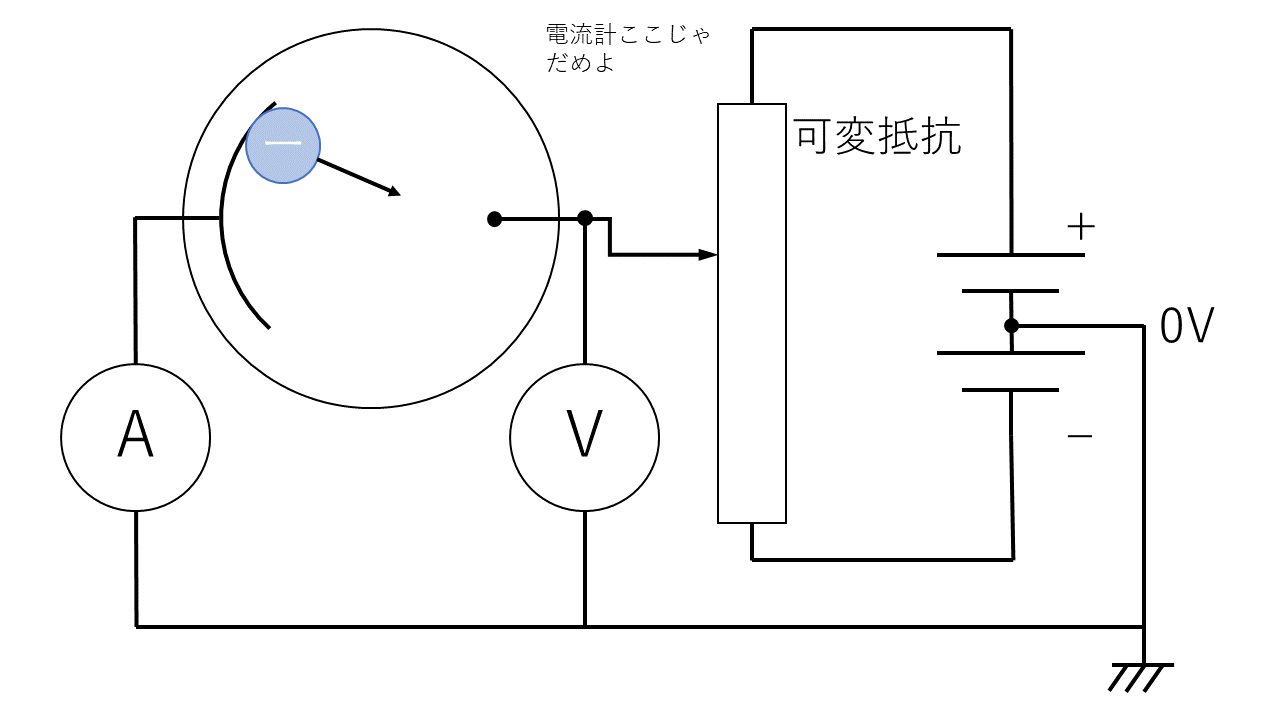
こんな回路を組みます.この回路は可変抵抗を動かすことによって電極A,B間の電圧を正負も含めて変化させることができます.
電極A側の電圧は常に0Vになるようにします.(これをアース接続と言います.)常に電極Aは0Vになるので,ここを基準にして考えます.
実験原理
光電子が飛び出して金属板から電極Bに到達すると,回路に電流が流れます.これを特別に光電流と呼びますが特に暗記不要なレベルで必要ありません.
光電流が流れる=金属板から光電子が飛び出している状態なので,当てた光の振動数は限界振動数\(ν_0\)を超えていることになります.
電子の経路はこんな感じになります.
電極Aについている金属板から飛び出した電子は,電極Bに向かって飛んでいきます.
無事電極Bに到達できた電子たちは電源の+に流れ込み回収されます.こうして電流が流れるわけです.
ちなみに,電流の流れる向きは電子とは逆なので,BからAの向きに流れます.
さらに,電極AとBの間に電位差が生まれる(Bの電位が0V以外になる)と,AB間に電場ができて,光電子もその影響を受けます.
電極A側は常に0ボルトなので,電極Bの電圧(極性)によって,光電子が加速されるのか減速させられるのかが決まります.
Bの電圧(電位)がプラスなら光電子は電極Bに向かう仕事を受けます.つまり加速されます.マイナスの電気を持った光電子が,プラスになっている電極Bに引き付けられるのは想像しやすいと思います.
一方,Bの電圧(電位)がマイナスなら,光電子は電極Aに向かう力(仕事)を受けます.マイナスの電気を持った光電子は,マイナスになっている電極Bから離れようとするのはイメージしやすいと思います.そうすると運動エネルギーは失われて減速し,Bにたどり着く前に運動エネルギーが0になってしまうと,電極Bから先に流れることはできなくなります.
電極Bに向かう際,電場による仕事に逆らった分は光電子が失った(電極Bがプラスの場合は「得た」)エネルギーに等しいので,電極Aから飛び出したとき光電子が持っているエネルギーを\(K_0\),電極Bに到着したときの光電子が持っている運動エネルギーを\(K_B\),与えられた仕事の大きさを\(I\)とすると,
$$k_B=K_0+I(電極Bの電位が正の時)$$
$$k_B=K_0-I(電極Bの電位が負の時)$$
$$Bでの運動エネルギー=Aでの運動エネルギー+電場による仕事(符号あり)$$
という式が出来上がります.
電極Bの正負によって電子が受け取る仕事はプラスかマイナスか変わってしまう点は注意が必要です.
仕事の符号の決定は,
- 電極Bがプラス→符号はプラス
- 電極Bがマイナス→符号はマイナス
となるだけなので問題ないでしょう.
電流が0になったとき
電流が流れなくなるということは,電子が電極Aから電極Bに到達できなくなったということを意味します.
電場が強くなると光電子が受ける力や仕事も大きくなり,最終的に光電子は電極Bに到達できなくなります.
先ほども書きましたが,電極Bに到達できない=運動エネルギーをすべて失ったということです.
光電子が電極Bにギリギリたどり着けない状態になった時の電圧を\(V_0\)とします.この時,電極Bでの光電子の速度は0なので,先ほどの式でいう所の\(K_B\)に0を代入してあげます.すると,
$$K_0=I$$
つまり,金属板から飛び出したときの運動エネルギーが電場からの仕事によってすべて失ったわけです.
この時の電圧\(V_0\)を阻止電圧と呼びます.
ここで,光電子が電場からされた仕事は\(eV_0\)なので,
$$K_0=eV_0$$
という式が成り立ちます.さらに,光電効果の公式から,光子の持つエネルギーを\(E\)とすると\(k_0=E-W=hν-W\)という関係がありますので,
$$E-W=hν-W=eV_0$$
となります.
それでは,今回の実験のまとめです.
- 光電流が流れるのは,光が限界振動数を超えていることが前提
- 光電管内は真空
- 光電管内の電場から受ける仕事と光電子の持つ運動エネルギーが等しいとき,ぎりぎり光電流は流れなくなる.この時の電圧を阻止電圧\(V_0\)と呼ぶ.
- 阻止電圧は,金属板の仕事関数Wと光の振動数\(ν\)に依存する

コメントを残す